Algo tienen las aves de corral para haberse convertido en parte imprescindible del recetario filosófico. Aunque el tema de hoy no es el manido “¿qué fue antes, el huevo o la gallina?” Si no lo que influenció a Nassin Nicholas Taleb para convertir el ejemplo del pavo antes de Acción de Gracias en un elemento más de la cultura popular: La gallina de Russell.
Bertrand Russell, el que para muchos es el filósofo anglosajón más influyente del siglo XX, se esforzó por eliminar de la filosofía las suposiciones que en su opinión resultaban absurdas e incoherentes. Esto le acabaría otorgando no solo un espacio entre los grandes filósofos de la historia, sino también un hueco en el corazoncito de muchos amantes de la Filosofía y, sobre todo, la Ciencia, que rehusaban seguir los complejos derroteros por los que se había ido la primera y que amenazaba con relativizarlo todo. Fue un puente crucial entre la filosofía tradicional y las corrientes analíticas porque transformó el enfoque filosófico al priorizar el rigor lógico y la claridad conceptual sobre las especulaciones metafísicas abstractas que caracterizaban a muchas de las escuelas previas.
Es muy probable que recurra a su figura en más ocasiones porque sus contribuciones en lógica matemática, especialmente a través de obras como Principia Mathematica (1910-1913) (en coautoría con Alfred North Whitehead), cimentaron los fundamentos de la lógica moderna, influyendo profundamente en áreas como la informática y la teoría de conjuntos.
Russell abordó una amplia variedad de temas filosóficos, pero vuelvo a su célebre ejemplo de la gallina (o pollo), que ya mencioné anteriormente para ilustrar las limitaciones del razonamiento inductivo. Por si se perdió ese capítulo, según este razonamiento, la gallina que recibe comida todos los días por parte del granjero acaba esperando que la rutina continúe indefinidamente, y asocia la presencia del granjero con alimento. Sin embargo, su visión inductiva del mundo no contempla que un día cualquiera esa misma presencia traerá consigo la muerte, una conclusión completamente inesperada dentro del marco de sus experiencias previas.
En este contexto, la probabilidad, una disciplina que encuentra su hogar entre la matemática y la estadística surge como una herramienta fundamental para evaluar la incertidumbre y tratar de cuantificar el riesgo en escenarios donde la inducción, por sí sola, no puede garantizar certeza. Pese a también depender de patrones pasados, permite modelar escenarios futuros con distintos grados de confianza. A través de su estudio, la humanidad ha desarrollado conceptos muy importantes y útiles que ayudan a medir la frecuencia esperada de ciertos eventos, salvando muchas vidas por el camino y ayudando al progreso.
Pese a que su estructura matemática proporciona una base más sólida para tomar decisiones en un mundo incierto, la probabilidad tampoco es infalible ante «cisnes negros». Porque ¿qué probabilidad puede tener algo que nunca se ha observado?
Midiendo lo incierto:
Decía Russel que la fuerza de las certezas aumenta en función de la repetición de casos observados, y he aquí el primer problema: ¿quién define cuales son los distintos casos posibles? Parece que las teorías y la experiencia previa son responsables, y aquí empieza a oler a más problemas.
En probabilidad se define el concepto de espacio muestral como el conjunto de todos los resultados posibles de un experimento o fenómeno aleatorio. Por ejemplo, al lanzar un dado de seis caras, el espacio muestral está compuesto por los números {1,2,3,4,5,6}. La probabilidad de cada evento individual dentro de este espacio puede variar según las condiciones y la información disponible, lo que conecta directamente con nuestro filósofo de día: cuantas más veces observemos un evento dentro del espacio muestral, más fuertes serán nuestras conclusiones probabilísticas, aunque nunca podamos alcanzar una certeza absoluta.
El espacio muestral puede estar incompleto, como por ejemplo en el lanzamiento de una moneda cuyo espacio muestral muchos definirían como {cara, cruz}, pero ¿es realmente imposible que caiga de canto? Es algo ciertamente improbable, pero si se lanzase sobre un terreno embarrado, dónde la moneda puede quedarse clavada, quizás se pudiese observar por primera vez tal evento «imposible». Aquí se corre el riesgo de pensar que lo que se ve es todo lo que hay, que dirían Daniel Kahneman y Amos Tversky, pero no suele ser una premisa válida para explicar cómo funciona la realidad.
Para intentar que el espacio muestral cubra el máximo número de opciones y las conclusiones sean lo más representativas posibles, es crucial considerar el tamaño muestral en los análisis, algo que también le recomendaría el propio Kahneman (para que vea que aquí no solo se habla de filósofos). Este concepto determina cuántos casos se deben observar o experimentar para garantizar que las inferencias sean confiables. Por ejemplo, si solo se observa un lanzamiento de un dado y sale un «6», se podría caer en la falsa conclusión de que “6” es el único resultado posible. Sólo al ampliar el tamaño muestral hasta realizar lanzamientos infinitos se podría deducir que todos los números del 1 al 6 son igualmente probables en un dado perfecto. En la práctica, con un tamaño lo suficientemente grande se confirmaría esa tendencia, pese a no conseguir un resultado perfecto.
Calcular el tamaño muestral mínimo necesario es, por tanto, una tarea clave para unir la teoría y la práctica. No se preocupe que esto no es se va a convertir en una clase llena de cálculos (aún). Obviando las fórmulas matemáticas, es importante mencionar que los siguientes factores afectan a la hora de calcular el tamaño de la muestra.
- Variabilidad de la población: Cuanto más variabilidad, mayor tamaño de muestra será necesario para que la aparición de casos menos probables se ajuste. En el ejemplo del dado todos los casos son igualmente probables, por lo que un tamaño comedido de la muestra puede arrojar resultados cercanos a la realidad. Por el contrario, la mayor variabilidad natural entre individuos hace que se den resultados poco significativos cuando se mide el desempeño académico en escuelas de pocos alumnos, sobrerrepresentando los casos extremos.
- Nivel de confianza: Cuanta más confianza se exija, mayor tamaño será necesario. Intuitivamente, la muestra tendrá que ser más grande para obtener un nivel de certeza del 99% que del 95%.
- Margen de error: Inversamente proporcional a la precisión exigida, es decir, cuánto se permite a los resultados que se alejen de la realidad. Cuanto menor margen de error, mayor será la muestra requerida.
- Tamaño de la población: La población, o grupo de interés del que se extrae la muestra, se refiere al total de individuos, eventos o elementos que comparten la característica específica que se desea medir. En el caso de la tirada de dados podría tratarse de los cientos de dados de un determinado casino. En el ejemplo de las escuelas, la población podría ser el conjunto de los estudiantes de un país, y el tamaño medirse en millones. Cuanto más grande sea el tamaño, mayor será la muestra necesaria.
Es bastante común encontrar literatura académica reconociendo que un tamaño de muestra insuficiente ha invalidado la credibilidad de ciertos experimentos. No se trata de una cuestión de vaguería de los investigadores, en muchos casos el tamaño de la muestra necesario puede hacer que un experimento sea imposible de realizar y haya que sacrificar alguno de los factores mencionados.
Fuera del mundo académico le resultará familiar el caso de los sondeos previos a las elecciones democráticas. Como referencia, en España el famoso CIS (Centro de Investigaciones Sociológicas) suele entrevistar a 4000 personas en edad de votar, cifra calculada a partir de un nivel de confianza de 95.5% y un margen de error del 1,6% para el conjunto de la muestra. Nunca he visto al CIS predecir que habría sobres con lonchas de chorizo en su interior, pero para alegría de los noticiarios suele haber alguna cada año, por lo que parece que el espacio muestral no coincide con la realidad en su totalidad.
También habrá algún que otro ejemplo en el que el CIS no haya acertado demasiado midiendo la intención de voto. Tampoco parece un trabajo sencillo por múltiples motivos. En primer lugar podemos echar mano al concepto de reactividad psicológica —fenómeno por el cual los individuos alteran su comportamiento o conducta cuando sospechan que están siendo observados—. Además se rompe el principio básico del secreto del voto, por lo que la pregunta no se ajusta a la acción en su totalidad, la encuesta no se hace el mismo día que la votación, no se conocen los incentivos de los entrevistados, y la variabilidad de las opciones es elevada debido a las circunscripciones. De hecho se observa que el error por comunidad es mucho más alto que el teórico utilizado para calcular el tamaño.
Podría uno llegar a pensar que hasta un mono lanzando dardos acertaría más veces. Aunque el ejemplo es robado del mundo de la inversión (al que acabaremos llegando), hay un último concepto pendiente antes de saltar a nuestra parcelita: ¿Qué hay de realidad en tal afirmación?
La tasa base: cuando todo lo demás no aporta
La tasa base tiene mucho que ver con la afirmación de los monos. Para explicar el concepto partamos del siguiente ejemplo: “puede llover”. Esta afirmación es bastante vaga y, sin más información, sólo se podría suponer que la probabilidad de lluvia es de un 50%, una estimación basada puramente en la incertidumbre. La tasa base (o prevalencia base) se refiere a la probabilidad inicial de un evento antes de considerar cualquier información adicional. En el ejemplo: 0.5 (50%). Sin embargo, este número puede cambiar a medida que se obtienen más datos.
Primer ajuste: Contexto geográfico
Si quienes participan en la conversación están en Sevilla en pleno agosto, intuirían que pueden ajustar su tasa base hacia abajo. La nueva tasa base se calibrará, partiendo de la primera, en función a la evidencia histórica relevante que dice que la lluvia en esa región y época del año es extremadamente rara. Esto estrecha la creencia inicial hacia una probabilidad mucho menor, quizás cercana al 1%, que será el siguiente punto de partida.
Segundo ajuste: Un dato nuevo
El servicio meteorológico andaluz informa de la existencia de un frente de baja presión que podría traer lluvias a la región. Este nuevo dato es una evidencia que debe combinarse con la tasa base anterior para calcular la nueva referencia. Imagine que según los meteorólogos, cuando llueve hay un 50% de probabilidad de que se den estos frentes. Esto no quiere decir que la nueva tasa base sea del 50%, sino que será el resultado de ajustar el 1% original con esta nueva información. Aquí entra en juego el teorema de Bayes, y en este caso sí es conveniente navegar un ejemplo práctico para ver por qué, dado que el ser humano es bastante malo trabajando con estadísticas y probabilidades.
El teorema de Bayes define la siguiente fórmula para calcular la probabilidad actualizada de A (la lluvia del ejemplo) dado que B (frente de baja presión):
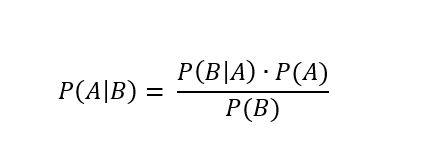
Donde:
- P(A) es la probabilidad inicial (la tasa base) de que ocurra el evento A, como la probabilidad de lluvia en Sevilla en agosto (muy baja). Para el ejemplo 0.01 (1%).
- P(B|A) es la probabilidad de observar la nueva evidencia B (frente de baja presión) dado que A es cierto (si llueve). Para el ejemplo pondré que van de la mano la mitad de las veces: 0.5 (50%).
- P(B) es la probabilidad total de observar B, independientemente de si A ocurre o no (frente de baja presión llueva o no, también improbable en Sevilla en agosto). Para el ejemplo 0.02 (2%).
- P(A|B) es la probabilidad actualizada de A (lluvia) dado que se ha observado B (frente de baja presión). Se denomina “probabilidad posterior”. Haciendo los números, la nueva tasa base es de 25%.
Puede pararse y hacer los cálculos a mano para ver dónde se ha ido el otro 25% que nos separa del número que intuitivamente esperaríamos encontrar.
Sólo encontraría un 50% si la probabilidad (tasa base) de frentes fuese exactamente la misma que la de lluvia, pero no es raro pensar que habrá ocasiones en las que haya frentes y no llueva (viento, nubes, etc.), y viceversa, llueva aunque no haya frentes. También podríamos obtener un 50% si la única causa de lluvia fuesen los frentes (P(B|A) sería 100%), pero aun así dependería de la relación entre frecuencias de cada evento.
Es posible que el ejemplo le haya creado cierto desconcierto si no está familiarizado con el tema (o si es meteorólogo y he dicho alguna barbaridad, ante la cual pido disculpas). La psicología cognitiva explica que nuestro cerebro no está feliz cuando algo resulta complejo de procesar. Para aliviar esa sensación de esfuerzo puede tomar algún dulce o seguir leyendo, porque le ofrezco un ejemplo más intuitivo (y alegre para paliar el desasosiego cerebral).
Tercer ajuste: Ropa mojada
Por la tarde, la misma persona se asoma por la ventana y ve que la ropa tendida está mojándose, este es otro dato adicional que eleva aún más la probabilidad de lluvia, sobre todo si suponemos que vive en una casa, lo que limita la opción de tener vecinos bromistas por arriba. Quizás, tras cotejar mentalmente esta nueva evidencia con la evidencia histórica de escenarios similares, la probabilidad haya subido hasta un 100%. Pero ¿Qué pasa con la tasa base?
- P(A) es la probabilidad inicial de lluvia en Sevilla en agosto, y no ha cambiado. Para el ejemplo 0.01 (1%).
- P(B|A) es la probabilidad de observar la nueva evidencia B (ropa mojándose) dado que A es cierto (si llueve, para el ejemplo es la única opción). Para el ejemplo 1 (100%).
- P(B) es la probabilidad total de observar B, independientemente de si A ocurre o no (ropa mojándose, sólo posible si llueve, así que la probabilidad es idéntica). Para el ejemplo 0.01 (1%).
- P(A|B) es la probabilidad actualizada de A (lluvia) dado que se ha observado B (ropa mojándose). Haciendo los números, la nueva tasa base es de 100%.
¿Por qué ahora sí? Porque B sólo puede darse si A. No hay otra opción (para nuestro espacio muestral) de que la ropa esté mojándose si no llueve, esto iguala la probabilidad de ambos eventos, algo que no pasaba en el anterior ejemplo. Aquí tenemos la tan manida causalidad (basada en la experiencia), no mera correlación.
Estos ejemplos ilustran cómo las nuevas evidencias van modificando la probabilidad inicial pero sin ignorarla. Combinar lo que ya sabemos con lo que estamos observando es crucial para evitar errores como sobrevalorar o ignorar determinados escenarios en la interpretación de eventos.
Para cerrar el bloque, es importante mencionar que el teorema de Bayes es una herramienta muy útil para el cálculo de probabilidades posteriores pero su extensión a teorema de rango como podría ser la lógica deductiva es muy problemática.
Invirtiendo: ¿Y ahora qué?
Una de las críticas al teorema de Bayes es que, si se es completamente objetivo, la probabilidad previa de cada evento es cero. Al haber infinito número de posibilidades, el cálculo de cada una no puede ser otro que cero. Por ello muchos bayesanos han abogado por el concepto de confianza subjetiva para poder justificar cálculos que intenten explicar la realidad. En la inversión la confianza subjetiva puede ser un obstáculo mayúsculo, en especial para el pequeño inversor ¿Qué confianza puede tener en no perder dinero?
Si no partimos de una probabilidad 0 (recomendable para no coquetear con el nihilismo), la experiencia previa dice que el pequeño inversor no lo tiene difícil si sigue ciertas buenas prácticas. Por otro lado, el análisis de las limitaciones inherentes al enfoque probabilístico dice que el pequeño inversor tampoco lo tiene fácil, y esa será seguramente la única conclusión que pueda extraer. Puede que el término conclusión no pasase una revisión mínimamente crítica al tratarse más bien de una obviedad, pero en ella reside una lección fundamental: la probabilidad es una guía, no una garantía. Aunque puede iluminar ciertos caminos, no elimina la incertidumbre ni asegura el éxito. El pequeño inversor debe navegar entre la confianza que brindan los números y la humildad de reconocer que siempre puede haber factores impredecibles que escapan a cualquier modelo probabilístico. Y sí, hacer caso al viejo adagio de «correlación no indica causalidad».
Cuando se dice que la renta variable a largo plazo devuelve un resultado positivo X, uno puede pensar en que la Primera Guerra Mundial fue para muchos, durante los primeros meses de conflicto, «la guerra que acabaría con todas las guerras». Quizás hasta tuviese cierto sentido probabilísticamente, como muchas otras cosas que acabaron no siendo ciertas. Otras, en cambio, eran incluso probabilísticamente imposibles, como que un activo digital sin garantía de ningún tipo hiciese millonarias a no pocas personas. Dependiendo de qué nos pregunten se podría decir que hasta cierto punto todo depende de la experiencia, pero en algunos casos se podría decir que nada dependerá de la experiencia previa, sino de la imposibilidad de conocer el futuro. ¿Entonces qué puede hacer uno para que la inflación no le coma los ahorros?
Puede asignar confianza a lo que dicen los estudios, y buscar flaquezas en tal asignación, aquí se le han presentado algunas herramientas. El espacio muestral es una de ellas, a la hora de definir en qué proceso se tiene más confianza, lo recomendable es al menos considerar un espacio lo suficientemente variado ¿Hay vida más allá de las carteras populares del momento? Si la probabilidad de que indexarse sea la mejor opción es alta puede preguntarse ¿Cuál es la probabilidad de que yo soporte la volatilidad? No olvide fijarse en el espacio muestral de su comportamiento, de poco sirve elegir al «caballo ganador» si no llega a meta montado, puede observarlo si se acerca al hipódromo, en ese caso ganará el siguiente que llegue a meta a lomos de su corcel, por lento que este sea.
También puede recordar el tamaño muestral, esto puede que no le haga ser el más popular de las redes sociales, donde se prodiga reducir el tamaño de la muestra lo máximo posible para que confirme un relato sesgado. «Tal fondo ha sido el mejor de los últimos años» ¿Y cuántos años son esos? ¿Qué pasó los otros años? Son preguntas que incomodarán a algunos, pero ayudan a asignar probabilidades.
Además es posible aplicar ambos conceptos al tiempo de una vida. Si uno escucha a los mayores es probable que oiga con asiduidad “si hubieras vivido lo que yo…”. Hay gente que ha encontrado tréboles de cuatro hojas, visto monedas aterrizar de canto y torres más altas caer, es importante prestar atención a sus vivencias, pues mejoran el cálculo de probabilidades ante lo que se podría definir sólo en base a la experiencia propia. Muchas ramas de la ciencia se fundamentan en ello. Esa conclusión también es obvia, pero no por ello deja de ser un buen consejo.
Si es de aquellos que se atreverían a reservar con muchísima antelación una noche de hotel para el 28 de julio de 2061, lejos de las luces urbanas, con el propósito de presenciar la próxima aparición del cometa Halley, usted confía en las probabilidades calculadas en base a la experiencia de otros y tiene medio camino hecho. El otro medio es exigir un grado de confianza similar a las predicciones que puedan hacerse en campos no tan científicos, como la bolsa o conocerse a uno mismo.
PS: El primer avistamiento del cometa Halley documentado data del año 240 a.c., no quiero decir con ello que tenga que exigir unos 2200 años más de recorrido a la renta variable para poder invertir.



Un artículo verdaderamente magistral, muchas gracias por publicarlo aquí. Supongo que lo tendrá en cuenta, pero, referido al tamaño muestral y su representatividad, es importante escoger bien la muestra. No sólo su tamaño, que también, sino sus características. Recuerdo un ejemplo de mi libro de Estadística, que podría explicarse más o menos así: imagine que hacemos una encuesta en el comedor de un colegio o universidad. Además, de escoger un número suficiente de alumnos, hay que atender a su origen y características. Y eso no supone distorsionar los resultados; sino lo contrario. Si el encuestador me pregunta a mi y a mis compañeros de mesa, es posible que obtenga unos resultados bastante parecidos en cuanto a gustos, opiniones políticas, etc. Sin embargo, cubriendo un mayor número de mesas, se pueden evitar, o minimizar este tipo de distorsiones (sesgos).
Muchas gracias por resaltarlo porque tiene toda la razón en que se me ha olvidado incluirlo. Es una de las partes más relevantes y es importante que quede también reflejada. En el ejemplo de CIS es como si se cogiesen los 4000 entrevistados del ya bastante estereotipado barrio de Salamanca, o del distrito de Vallecas.
También es importante resaltar que hay que tener en cuenta estudios y análisis previos para poder elegir qué variables son relevantes y cuales no. Es ahí donde más fácilmente se ve un ejemplo de convergencia de la estadística descriptiva y la inferencial. Gracias a la estadística descriptiva (la que simplemente describe los atributos del sondeo) se puede ver si es importante buscar una muestra variada en cuanto a edad, barrio, municipio o por el contrario color de coche y número de letras en el nombre de pila.
Excelente artículo. Ha sabido sintetizar las fortalezas y las limitaciones de la estadística en el proceso de decisión. Si me permite agregar algunas reflexiones que me iban surgiendo a medida que avanzaba en la lectura:
A mi juicio, uno de los principales errores a la hora de aplicar la probabilidad en la toma de decisiones es no tener en cuenta el “impacto” del evento. En la práctica, la probabilidad de que suceda un evento tiene que ajustarse en relación a su magnitud. Un evento muy poco probable pero cuyas consecuencias sean excepcionales merece mayor consideración de la que se le presupone matemáticamente. Merece la pena protegerse de un evento cuya probabilidad sea <1% si el resultado es, por ejemplo, la bancarrota. En el otro sentido, jugar a la lotería deja de ser irracional si en lugar de emplear la estadística bruta la ponemos en correlación con la magnitud del evento. El downside es mínimo (unos pocos euros al mes) pero el upside es potencialemente de los que te cambian la vida. Claro que, en ambos casos, el cálculo implica tener en cuenta los costes y el coste de oportunidad de las alternativas.
Una de las conclusiones que se derivan de los trabajos en el campo de la economía conductual es que los seres humanos somos pésimos cuando se trata de razonar estadísticamente. Principalmente porque las estadísticas no son para nada intuitivas, en muchas casos hasta contraintuitivas, y suelen entrar en conflicto con nuestras emociones. Pero aquí se abre una cuestión más fundamental: basta con la pura estadística para tomar mejores decisiones? Qué papel tienen las emociones en la toma de decisiones? Antonio Damasio tiene un libro muy bonito titulado “El error de Descartes”. Tras el estudio de lesiones cerebrales y aplicando los conocimientos en neurociencia, llega a la conclusión de que las emociones son claves para la racionalidad del comportamiento. Que las personas con sus facultades cognitivas intactas pero con dificultades emocionales (tanto por exceso como por defecto) toman sistemáticamente peores decisiones. Una de las tesis del libro es que las emociones proporcionan una información valiosa que, bien canalizada, permite mejorar la toma de decisiones. Quizás tomar decisiones en la vida en base únicamente a las matemáticas no sea la mejor opción.
La probabilidad es un concepto epistemológico, no ontológico. Es la forma matemática que utilizamos para cuantificar la ocurrencia de eventos, pero no es una propiedad de los eventos. Cuando un evento tiene un 50% de probabilidades de ocurrir y un 50% de no ocurrir, no quiere decir que, ante identicos condicionantes causales, el evento pueda ocurrir o no ocurrir aleatoriamente, sino que no conocemos todas y cada una de sus causas y su relación entre ellas que llevan a que se materialize esa probabilidad. Yo hasta la fecha rechazo la aleatoriedad ontológica ya que implicaría sucesos sin causa o paradojas como la del gato de Schrödinger en que el que algo existe y no existe simultáneamente (y esto es un imposible lógico según el principio de no contradicción). A menudo se suele decir que la mecánica cuántica ha demostrado el carácter indeterminista de la materia a escala subatómica (principio de superposición, dualidad onda partícula, principio de incertidumbre). Sin embargo, cada vez hay más interpretaciones realistas de la cuántica que rechazan la interpretación de Copenhague (ya el propio Einstein era un furibundo crítico de ese indeterminismo de la cuántica, de ahí su famosa frase “Dios no juega a los dados”, que mucha gente interpreta en sentido teológico cuando era una forma poética de criticar el indeterminismo). Las interpretaciones realistas nos dicen que la formalización probabilística de la cuántica no implica que la naturaleza sea esencialmente indeterminista en un sentido absoluto. Es la consecuencia de la forma en que formulamos y aplicamos la teoría. Es decir, la superposición de un electrón (que esté en dos posiciones diferentes al mismo tiempo) antes del colapso de la función de onda es epistemológica. No implica que, efectivamente, el electrón esté en dos lugares al mismo tiempo sino que sólo podemos predecir probabilidades de los diferentes estados. Se suele confundir aleatoriedad con indeterminismo. El ejemplo prototípico de experimento aleatorio es el del lanzamiento del dado. Aparentemente ejemplificaría la aleatoriedad ontológica. Aunque sea un proceso físico determinista con una distribución de probabilidad bien definida para una colección de eventos los suficientemente amplia, aparentemente es imposible predecir el resultado de cada evento individual. Sin embargo esto no tiene que entenderse como que la trayectoria del dado esté incausada (como si de repente el dado cambiase de dirección sin causa). Significa que nos encontramos ante un evento caótico extremadamente sensible a la condiciones iniciales. Condiciones que, en la práctica, es prácticamente imposible de conocer.
Como sé que es amante de la filosofía, me voy a meter en un berenjenal filosófico: es cierto que negar la aleatoriedad ontológica lleva a una postura predeterminista fatalista que postularía que, conociendo exactamente todas las condiciones iniciales de un sistema, sería posible conocer el futuro de ese sistema (y esto nos lleva a toda una serie de problemas filosóficos cuando nos situamos en una categoría antropológica). Pero a mi juicio sigue siendo un resultado preferible al de tener que aceptar la causa sui de ciertos eventos. Una cosa indeterminada significa por definición que no está determinada por unas causas iniciales. Si esa cosa aparece o cambia de estado sin atender a causas quiere decir entonces que ella misma es la propia causa de su cambio. Y esto nos lleva a una paradoja lógica por la cual para que una cosa se cause a sí misma esa cosa tiene que empezar a existir antes de que exista. Si el momento del cambio orbital de un electrón no depende de ninguna causa (que es lo que postula la interpretación de Copenhague de la cuántica) entonces este fenómeno es causa de sí mismo (sería como postular que ante las mismas condiciones ambientales el agua contenida en un vaso “decida” pasar de un estado líquido a un estado sólido aleatoriamente). Es por eso que este tipo de interpretación tiene que aceptar que el electrón está y no está (realmente y no probabilísticamente) en varios lugares simultáneamente. Y lo tiene que hacer a nivel ontológico, porque si lo hace a nivel probabilístico simplemente está reconociendo que es una cuestión epistemológica. Hay ciertas personas que intentan resolver esto haciendo la distinción entre determinismo y predeterminismo. El determinismo implica que las cosas siguen la estricta legalidad física pero que no están predeterminadas, es decir, que son contingentes. Pero a mi juicio esto no resuelve el problema. Porque si son contingentes en un sentido epistémico significa que es una cuestión de nuestro conocimiento. Y si es una contingencia ontológica sigue sin explicar porqué, ante unas mismas condiciones, una cosa puede darse o no darse. La postura predeterminista tiene también sus problemas, pero como mínimo tenemos constancia a nivel atómico y molecular de sistemas predeterministas (somos capaces de predecir ciertos eventos conociendo las condiciones iniciales). El problema es como compatibilizamos esto con los saltos categoriales, es decir, sin reducirlo todo a ciertas condiciones iniciales de la materia a escala atómica o incluso subatómica. Sin embargo no conocemos a nivel atómico ningún ejemplo de causa sui. Y, de hecho, cuando aparentemente se nos presenta un evento sin causa sencillamente aceptamos que existen unas variables ocultas que aún no conocemos. Tiene más sentido pensar que es lo que ocurre también a escala subatómica.
Muchísimas gracias por su respuesta y sus reflexiones que son estupendas.
A mi esta distinción me gusta manejarla cuando hablo de riesgo en la toma de decisiones, por la trillada definición de
Riesgo = probabilidad * impacto
Aunque esto es simplemente un gusto personal, porque uno puede cambiar lo que pone a la derecha y a la izquierda de la ecuación a su gusto. No dejaría de ser igualmente defendible que el éxito dependa de la probabilidad y el impacto, como bien defiende (aunque aquí uno suele ser más humilde y reconocer que habría que sumar la suerte). El no mezclar probabilidad e impacto es por el mero hecho de darle la importancia que considero tiene, independientemente del valor de sus predicciones. El teorema de Bayes lo hace bien “se arruine uno o no” (lo cual depende del impacto).
Y abre usted un melón de los más jugosos alrededor de que la Probabilidad sea un concepto puramente epistemológico que describa el conocimiento de algo y no una propiedad intrínseca de ese algo. Intentaré explicarme lo mejor posible, porque no es una conversación que tenga muy a menudo y mis pensamientos carezcan de orden.
Mi motivo para abrazar en ocasiones el lado ontológico parte de lo que seguramente parezca y sea una incoherencia, y tiene que ver con la construcción lineal del tiempo. Y aquí verá que en realidad estamos juntos porque lo que usted piensa de la probabilidad lo puedo llegar a pensar yo del tiempo lineal (sin el cual no entiendo la Probabilidad). Concretamente de lo que los griegos llamaban Kronos, esa concepción del tiempo como una secuencia ordenada y continua de eventos, en la que el pasado precede al presente y al presente le sigue el futuro.
Aquí el debate ontológico / epistemológico tiene que ver con si el tiempo lineal es una realidad objetiva que existe independientemente de los seres humanos (una “entidad” o “dimensión” del universo) o si es simplemente una construcción humana utilizada para ordenar los eventos (una herramienta epistemológica). Para nuestra cuestión, yo veo aquí la fuente primaria de la discusión probabilística, es decir, si la probabilidad es o no ontológica, depende de si el tiempo lo es. Y por mi paz mental, cuando veo tal relación pongo en cuarentena los hilos mentales del tipo “asumo que ambas tienen la misma naturaleza”. Es decir, usted deja ver que considera el tiempo lineal un concepto ontológico, y de ello se deriva una probabilidad epistemológica. Para mi eso tiene sentido, pero también la combinación opuesta.
En general para las cuestiones científicas de este tipo, donde la única diferencia entre un estado y otro de un determinado objeto u evento es cuestión de tiempo, me ayuda pensar ¿Qué pasaría si el tiempo no existe de hecho? Y ahí usted se protege mejor que yo, que abrazo ese caos con demasiada alegría. Porque ahí es necesario hablar del gato y de la convención de Copenhague, ya que si percibimos que algo tiene dos estados, y el tiempo no existe como lo conocemos, por necesidad tiene que estar en ambos estados (o más) simultáneamente. Por ese motivo me resulta especialmente cautivadora la cuántica, además de por el campo en sí, por la potencial vía de conocimiento del tiempo. Pero ¿Se puede andar por la vida realmente pensándolo? Lo dudo mucho, de ahí que hasta los más grandes científicos subrayasen las carencias de esta aproximación.
La alternativa es más atractiva, pero no está libre de problemas, como bien plantea usted.
Ante tales problemas uno opta por una variación más “suave” de la pregunta del tiempo ¿Qué pasa si el tiempo sí existe de hecho pero la percepción transitiva es lo que hemos construido? Uno abraza el determinismo con fuerza cuando coquetea con tales posturas. Y fíjese que habla usted de conocer el futuro, pero en realidad ese sería casi el menor de los problemas, porque conociéndolo o no, todo da lo mismo. Podemos gritar que tenga cuidado al protagonista de la película que estamos viendo, pero no cambiaría nada.
Verá que no me mojo mucho en una postura u otra porque soy bastante ignorante y ambas me hacen tilín, pero ninguna tolón. A lo largo de los artículos del blog igual saco alguna cosa más en claro al darle más vueltas al asunto, porque sí tengo cosas preparadas sobre relatividad, ontología, el señor Schrodinger y algo que viene pronto sobre el paso del tiempo en función de la gravedad.
¿Falsa dicotomía?
¿Lo cree o lo sabe?
El principio de no contradicción no es absoluto, simplemente es una herramienta. Pero si le parece importante mantener ese principio, ahí tiene teorías como muchos mundos etc que le darían un enfoque diferente, aunque no describan por ello mejor la realidad mantendrían este principio a flote.
Pasando a cuestiones más concretas, la paradoja del gato de Schrödinger ( así como otras de la época como LPR etc ) son ejemplos llevados al extremo para ilustrar ciertas debilidades de la mecánica cuántica, en este caso traen a la palestra cual es la conexión entre el mundo cuántico y clásico, cuando se pierden o no las propiedades cuánticas y que lo que en un mundo tiene sentido en el otro resulta absurdo. No hay que tomarse literalmente esta interpretación, no significa literalmente que el gato esté muerto y vivo al mismo tiempo, hay varias explicaciones para esto, por ejemplo mediante la decoherencia.
Cómo le gusta a ud. diferenciar entre lo que es ontológico y epistemológico, va a llegar a un punto en el que nada de lo que le rodea tenga entidad ontológica.
A mi me parece que en toda su argumentación existe cierta circularidad, la lógica clásica no tiene por qué ser la mejor herramienta para entender fenómenos complejos como partículas cuánticas o fenómenos emergentes, just saying.
Ya que está metido en harina, me gustaría conocer como definiría usted el tiempo, concepto intrínsecamente ligado a muchas cuestiones que menciona sobre causalidad o el determinismo.
En otras palabras, la esperanza matemática.
Aunque no sea una línea clara , yo creo que la gente se lía comparando probabilidades en física con probabilidades en economía.
Al final son un tipo de probabilidades distintas. Unas se pueden reproducir de modo experimental si es necesario y las otras no.
En unas es lícito suponer que no van a cambiar por las meras condiciones del entorno y en las otras es incluso delicado suponer que los actores que interpretan dichas probabilidades no terminan provocando todo tipo de fenómenos que las alteran.
Fíjense en el riesgo de los préstamos hipotecarios. Un banco puede utilizar datos históricos por un lado para vender las virtudes de un producto titularizado de muchas hipotecas para clientes que compran ese tipo de deuda. Pero por el otro puede dar hipotecas con unas condiciones mucho menos estrictas que las históricas.
También vemos con frecuencia extrapolaciones de datos históricos de incluso 30-40 años o más. Pero luego parece que no hay ni interés en mirar esos mismos datos a más plazo o en que medida se han ido alterando esos datos a lo largo de la historia.
Nos solemos olvidar que la llamada física clásica ya tenía problemas simplemente en conjugar la física newtoniana con la teoría electromagnética.
Precisamente dada su importancia histórica, es fácil terminar confundiendo la lógica clásica con simplemente la lógica de las ideas newtonianas. Y esas ideas suelen terminar siendo problemáticas cuando aparecen fenómenos de tipo ondulatorio.
Vamos que a veces donde no se aceptan postulados de tipo en realidad no se termina de entender a fondo las nociones de fenómenos donde es importante entender algo más que las partículas.
También podría pasar a la inversa en quien sólo entendiera los fenómenos ondulatorios y no los de partículas. Pero ese caso en la práctica no tengo claro que exista de modo general aunque sí luego se intentaba aplicar a ciertos fenómenos de modo clásico en el ámbito de dichos fenómenos en teoría ondulatorios.
Sin necesidad de meterse en las complicaciones teóricas de la mecánica cuántica, simplemente metiéndose uno a analizar los experimentos de la llamada física cuántica, que no dejan de ser situaciones históricas donde se empezó a ver las limitaciones de los enfoques clásicos, ya se puede intuir que el típico enfoque lógico anterior no sirve para lidiar con esas situaciones.
Para no repetirme y dado que sus comentarios guardan relación con las objeciones que me ha hecho @AlanTuring intentaré responder a ambos conjuntamente.
Si me pregunta si lo sé a ciencia cierta como quien sabe que 2+2=4 la respuesta es no, no tengo como demostrarlo. Es más bien una afirmación como consecuencia de ciertas premisas que me resultan intuitivamente más plausibles, como la ausencia en la realidad de fenómenos que se causan a sí mismos o la idea de que, si un efecto está directamente relacionado con su causa, no veo cómo unas mismas causas, idénticas en cualquier sentido, por muy complejas y entrelazadas que estén, pueden dar lugar a dos efectos distintos. Viola directamente principios intuitivos y lógicos como el principio de razón suficiente o el principio de causalidad proporcional. Sin perjuicio de que el determinismo absoluto tiene sus propios problemas como el del colpaso modal (todo lo que existe es necesario) y como hacemos para encajarlo a una escala antrópica y la idea de la aparente libertad (y por lo tanto contingente) que tenemos los seres humanos. Es en este sentido que saqué a colación la mecánica cuántica, puesto que es la principal (y única a mi entender) herramienta científica que probaría la contingencia ontológica. Obviamente es un asunto complejísimo que en muchos aspectos supera mis capacidades. Principalmente en su formalismo matemático que es esencial para entender la teoría. Muchos de sus conceptos son puras entidades matemáticas que solo podemos llegar a transmitir muy vagamente en lenguaje natural. Pero hasta dónde he podido indagar mediante la lectura de libros y papers y escuchando a personas que se dedican profesionalmente al campo de la cuántica, gran parte de las ideas extravagantes que suelen citarse en la divulgación de la cuántica desaparecen cuando se hace una mejor interpretación de la interpretación de Copenhague. En este sentido, para ser honestos, el problema no es tanto la interpretación de Copenhague como ciertas interpretaciones de la interpretación de Copenhague. Interpretaciones que, por cierto, llevaron a que grandes nombres dentro de la física despreciaran la cuántica. Ya he citado a Einstein. Otro podría ser Richard Feynman y su famosa frase “si cree que ha entendido la mecánica cuántica es que no la ha entendido”. Entre esas cosas que oscurecieron el campo y que seguro todos ustedes han escuchado alguna vez podemos citar la supuesta subjetividad del colapso de la función de onda (ya saben, aquello que dice que lo que hace que se defina una partícula es la presencia de un observador), la idea de que a escala cuántica una partícula puede estar en dos lugares al mismo tiempo (cuando la superposición es probabilística, no real) o el fenómeno de entrelazamiento cuántico (dos partículas separadas por millones de kilómetros se definirían simultáneamente, violando la ley física de que no se puede transmitir información a velocidades superiores a los de la luz. En realidad se refiere a la medición de ciertas propiedades restringidas de un sistema).
El principio de no contradicción es un principio fundamental de la lógica. Establece que una proposición no puede ser falsa y verdadera al mismo tiempo y en el mismo sentido. A mi juicio no hay forma de negar el principio de no contradicción sin caer en absurdos. Cualquier razonamiento o argumento tiene que presuponer el principio de no contradicción. Además, negar el principio de no contradicción es una paradoja autorreferencial: si aceptamos que las contradicciones son posibles (es decir, que una afirmación puede ser tanto verdadera como falsa al mismo tiempo y en el mismo sentido), entonces la afirmación “el principio de no contradicción es falso” también puede ser tanto verdadera como falsa al mismo tiempo y en el mismo sentido. El enunciado se autorefuta. Es como el enunciado “toda verdad es subjetiva”. Si esta afirmación es verdadera entonces ella misma es subjetiva, lo que implica que podría no ser cierta. Y si es universalmente cierta entonces es que existen las verdades objetivas (y por lo tanto también se refuta). A mi juicio, para poder entablar cualquier conversación hay que presuponer que no son posibles las contradicciones lógicas. El análisis lógico de un enunciado es el primer cortafuegos para saber si una afirmación tiene sentido o no. Muchos argumentos o teorías se desechan simplemente porque llevan a contradicciones lógicas insalvables, como por ejemplo temas relacionados con la existencia de Dios, que sólo se pueden refutar mostrando las contradicciones lógicas de la idea de Dios (por lo menos el del Dios bíblico). No quiero decir con esto que es suficiente con que un enunciado sea lógicamente verdadero para que su contenido sea verdadero. Pero lo contrario si es cierto: si un enunciado es lógicamente falso entonces su contenido no puede ser verdadero.
No tengo una definición de tiempo con la cual me comprometa necesariamente. Ontológicamente parece ser que la teoría que mejor describe la naturaleza del tiempo es la que se deduce de la mecánica relativista: el tiempo como una dimensión fundamental de la realidad en la entidad “espacio-tiempo”. Eso es lo que describe la teoría de la relatividad y lo que comúnmente está aceptado y comprobado experimentalmente (el experimento de los relojes atómicos que prueba la dilatación del tiempo, la desviación de la luz por la gravedad que prueba la curvatura de la dimensión espacio-tiempo o la detección de ondas gravitacionales que prueban la vibración del “tejido” espacio-tiempo).
Ahora, de la teoría de la relatividad se deriva una teoría filosófica del tiempo que es poco compatible con como lo experimentamos los humanos. En la filosofía del tiempo se aceptan comúnmente dos grandes teorías: la Teoría A del tiempo y la Teoría B del tiempo. Sin entrar mucho en detalle, la Teoría A es una teoría tensional del tiempo: nos dice que existe un flujo temporal y que las cosas y eventos únicamente existen en el presente. El pasado dejó de existir y el futuro aún no existe. El tiempo es por lo tanto objetivo. La principal corriente dentro de la Teoría A es el presentismo. La Teoría B del tiempo es una teoría atensional del tiempo: nos dice que el flujo temporal no existe. Pasado, presente y futuro son igualmente reales. El flujo del tiempo sería entonces un fenómeno psicológico que experimentamos los seres humanos, pero no una realidad objetiva. La principal corriente de la Teoría B, y que se contrapone al presentismo, es el eternalismo. Lo curioso de esto es que la teoría más compatible con la idea de “espacio-tiempo” de la mecánica relativista es la Teoría B del tiempo, que, sin embargo, es la intuitivamente menos obvia de las dos. Esto es así porque la Teoría A del tiempo requiere de simultaneidad temporal y sin embargo sabemos que el tiempo es relativo dependiendo de las condiciones del observador: no existe un presente universal (cuando miro el sol en mi presente estoy observando el presente del sol hace 8 minutos y 20 segundos que es el tiempo que tardan los fotones en recorrer la distancia hasta la Tierra). Hay otras críticas a la Teoría A del tiempo como la paradoja de Andrómeda que expuso Roger Penrose o la idea de que, dado que la unidad de tiempo más pequeña es el tiempo de Planck que equivale a 5.39 × 10â»â´â´ segundos, en realidad lo único que existiría a escala humana es el pasado, por el hecho de que en el instante que pienso en el presente este ya es pasado. El eternalismo tampoco está libre de críticas como por ejemplo el problema de la experiencia del presente, conflictos con la noción de entropía en la termodinámica (si no existe flujo del tiempo como se justifca la segunda ley de la termodinámica que dice que en un sistema cerrado la entropía tiende a aumentar con el tiempo?) o qué entendemos entonces por “existir”.
En cualquier caso, cualquiera de esas dos teorías no compromete el principio de causalidad ni el determinismo puesto que ambas entienden los eventos como sucesos ordenados en el tiempo. Si me pregunta por cual me decantaría ahora mismo, me cuesta no aceptar la realidad del flujo del tiempo, por lo tanto por la Teoría A, pero al mismo tiempo soy consciente de que la Teoría B explica mucho mejor fenómenos que observamos en la realidad… salvo nuestra experiencia subjetiva.
El problema de basar las argumentaciones en la intuición y causalidad proporcional es que está dando por sentado muchas cosas.
Los experimentos basados en las desigualdades de Bell han confirmado la existencia de correlaciones no locales sin que ello implique una violación de los principios causales, sino que demuestran que la estructura del espacio-tiempo y la causalidad en el ámbito cuántico deben ser interpretadas de forma diferente a la intuición clásica.
¿Lo cree o lo sabe? ¿En qué punto se encuentra un electrón que es una onda? ¿Ha realizado el experimento de la doble rendija y ha llegado a la conclusión de que no es real?
No. El principio de no contradicción no es un principio fundamental de la lógica, sí lo es de la lógica clásica como ya indiqué en mi comentario previo.
Existen muchas áreas del conocimiento que admiten contradicciones para reflejar la complejidad de la realidad y no por ello caen en absurdos.
La diferencia radica en que, no por que exista una contradicción todo deba ser desechado y se considera que todo puede ser verdadero. La lógica clásica tiene otro ámbito de aplicación. La rigidez de este sistema de pensamiento no deja de tener un objetivo pragmático pero no es una verdad inmutable sobre la verdad del razonamiento.
Noto en sus argumentaciones parten de premisas sobre las que aún hay un gran debate abierto, por lo tanto, no puedo dejar de apuntar que asumir como verdaderas ciertas cosas es cuanto menos osado.
Por ejemplo, conceptos como el colapso de la función de onda, la superposición y el entrelazamiento, aunque poco intuitivas, son la base de nuestra civilización actual y han sido objeto de amplias investigaciones que han llevado a interpretaciones más sofisticadas sin renunciar a la consistencia teórica y empírica, con esto no quiero decir que que a medida que avance el conocimiento se cambie la percepción que tenemos pero de momento todo son interpretaciones.
No estoy negando que existan los fenómenos de colapso de la función de onda o el entrelazamiento cuántico. Lo que niego son las interpretaciones que se hacen de esos fenómenos. Y ojo, no lo niego gratuitamente. Me baso en multitud de fuentes que explican esos fenómenos sin recurrir a la mística divulgativa en la que se vio envuelta la cuántica. Podría intentar explicar yo mismo cada uno de esos fenómenos pero prefiero dejar, por una cuestión de comodidad y claridad, unas capturas de un libro divulgativo de Carlos Sabin, doctor en física e investigador en el Instituto de Física Fundamental en el CSIC, titulado “Verdades y mentiras de la física cuántica”. Reitero que esto mismo que se explica en las capturas es algo que he leído y escuchado de otras muchas fuentes. Por cierto, el interés de este autor se centra en la tecnología cuántica y el libro tiene un capítulo muy interesante dedicado al tema.
El libro desmitifica también otros conceptos como la dualidad onda-partícula, el experimento de la doble rendija, el papel del observador en el colapso de la función de ondao la incertidumbre. Pero para no hacerlo pesado, y como el libro se puede encontrar fácilmente en formato pdf en internet, creo que esas capturas bastarán para hacerse una idea de lo que estoy intentando exponer. La cuántica es un campo complejísimo, y aún no acabamos de entender bien como se comporta la materia a esas escalas, pero se han cometido ciertos abusos del lenguaje a la hora de intentar explicar y divulgar lo que se observa a escala cuántica que han llevado a ideas e interpretaciones erróneas.
Como curiosidad, en el que es considerado el manual académico canónico en el campo de la cuántica “An introduction to quantum field theory” de Peskin y Schroeder el concepto “dualidad onda-partícula” no aparece mencionado ni una sola vez en sus más de 800 páginas. Esta distancia entre las ciencias académicas y la divulgación científica no es exclusiva de la física cuántica. Ocurre en todas las ciencias. Para hacer digerible y explicable para el gran público lo que ocurre dentro del campo científico a menudo se tiene que recurrir a metáforas, analogías, simplificaciones y abusos del lenguaje. En física, y más aún en física cuántica, dada su complejidad y el uso de las matemáticas como fundamento de muchas teorías, esto está llevado al extremo. El problema es cuando todo ese lenguaje divulgativo se toma al pie de la letra y no como lo que es: la forma de poder transmitir al gran público la ciencia. Entonces aparecen malos entendidos como partículas que se transforman en ondas, superposiciones reales o información que se transmite instantáneamente.